|
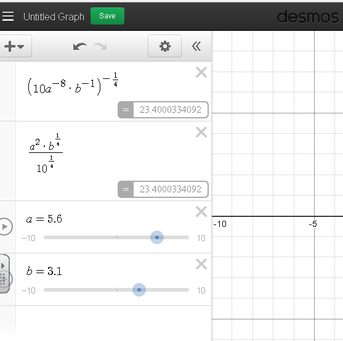
Over the past couple of weeks I have been posting about the quadratic unit that we are covering in my freshmen math class. Today I am going to deviate from that a bit to talk about a lesson that occurred today. The first part of the next unit is using exponent rules to simplify expressions. There are a lot of mechanics involved, and the practice problems can get quite tedious. Lately I have been telling my freshmen that teachers are like personal trainers. I gave them this scenario: imagine you go to the gym with your personal trainer. For an hour you watch your trainer run 5 miles, then afterwards you watch them lift weights. At the end, you leave the gym and say that you "worked out." Ridiculous right? The personal trainer should show you some exercises and guide you to best practices, but at some point you need to perform those exercises and routines yourself, and go through the sweat and tears. Teaching and learning is much like that. The teacher can guide and show certain things, but the students must perform the exercises and go through the sweat and tears much the same way as in the gym. I thought to myself: 'How can I guide my students through these exponent rules while giving them the opportunity to go through the sweat and tears necessary to deepen their learning?'  First, I created examples for them and handed them out. Above is one of the examples that I gave the students. You can download the full worksheets here. As you can see, the worksheet isn't anything special - it is something that I've more or less handed out every year. I then organized the class in to six groups using the Team Shake app. You can see the organization of the teams on the right. After the class re-organized themselves in teams, I said the following: "Okay, all of you are in your teams. Team 1 is responsible for Example 1 in the packet I gave you, Team 2 is responsible for Example 2, and so forth. Your team needs to think about the problems in your example and talk together to determine how to do them. Perhaps some of you have seen this before and you can start the group in that direction, or maybe you want to go to www.wolframalpha.com, type in your question, see the answer, and then work backwards. As always, you can ask me well thought out questions. In addition, each team gets one "spoon feed" - I will work out ONE example for you if your group requests it. I won't tell you what I am doing, though, it will just be the work and process written on a small white board. Okay - enjoy!" I left the team arrangements showing on the screen. The students went off in their teams and began their problem set. Here are the things I observed:
0 Comments
|
Archives
February 2021
Categories
All
AuthorJeff Watson is a Math teacher at the International Academy East in Troy, MI. His work as a software engineer made him realize the need for problem solvers and critical thinkers in the workplace today. Jeff believes that the secondary math classroom should be a place of critical thinking, collaborative learning, and exploration which will cultivate the problem solvers and thinkers needed today. |


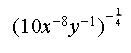





 RSS Feed
RSS Feed
