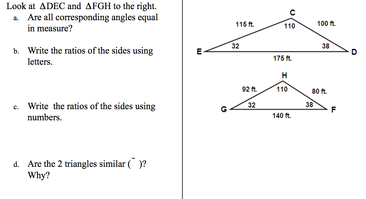
 Figure 1 Figure 1 Recently we started a lesson on similar triangles. I thought a lot about what to have the kids do, and a small part of me (very small) wanted to 'direct teach' the lesson to save time - we are behind, after all, and if I just told them what similar triangles were and what to do with them we could move on to the next lesson. In the past, I would typically give them scripted notes that had a set of similar triangles, such as the example in figure 1. I would explain what similar triangles were, and how to find different things about them, such as angle measures and/or side lengths. The students would typically do well with this and then we could say that we had 'learned' similar triangles. This year I wanted to provide a richer opportunity for them. I put up the following directions:
I purposely made the direction vague. Some students asked me what similar triangles were, but I pushed it back to them to use their resources, such as their phone, computer, or textbook, to figure it out. Some students also asked what I meant by a 'set' of similar triangles. I asked them to look up that word as well and then decide what to do. I had to laugh because some students just really needed me to tell them 'how many' triangles they needed to make. I did not want to tell them because I did not want to give them a threshold at which to stop learning. As time passed, many students were using their protractors to create two triangles that had the same angle measures. Two seemed to be the most popular number of triangles. There were a lot of struggles going on as measurements were being made and sides were being measured. Some students used a lot of paper, while others used a sheet or two. With about ten minutes to go in the block, two of my students, Filip and Haden, asked me to come and look at their set. I walked over to their desk and this is what I saw: Needless to say, I was floored! The expectation in my head was to see two triangles that were created using straight edges and rulers. I of course inquired about what had happened and what led them to this result, and I found out what actually happened: they used one sheet of paper and created thirteen (or so) triangles in about 5 minutes. All of the triangles were similar, but the beauty of it was that they did it by folding the paper - rulers and protractors were not needed (one is shown in the picture, but it wasn't used). The best part was that I was going to demo to the whole class how to 'quickly' create two similar triangles (by overlaying them on each other), and instead I had these two students demonstrate a much more powerful demonstration.
I was really thankful afterwards that I didn't give in to the urge to instruct directly because this opportunity would have been completely lost. Instead, it was gained, and was a nice lead in for the next class, as I had Haden and Filip lead the class on how to construct so many similar triangles in such a short time.
0 Comments
Your comment will be posted after it is approved.
Leave a Reply. |
Archives
February 2021
Categories
All
AuthorJeff Watson is a Math teacher at the International Academy East in Troy, MI. His work as a software engineer made him realize the need for problem solvers and critical thinkers in the workplace today. Jeff believes that the secondary math classroom should be a place of critical thinking, collaborative learning, and exploration which will cultivate the problem solvers and thinkers needed today. |



 RSS Feed
RSS Feed
