|
Before we embark on day 4, here is a quick summary of the first three days of the unit:
Day 1: The students used Desmos polygraph to discuss the vocabulary surrounding the graphs of quadratics. Day 2: We used the +1 Routine to generate all of our thinking about parabolas and quadratics. This led to the Desmos marble slides activity where the students wrote equations of quadratic functions in vertex form in order to generate graphs that 'catch' stars. Day 3: The students continued the marble slides activity by plotting the vertex on each page of the activity, converting the equations from vertex form to standard form, and looking at the 'wideness' and 'narrowness' of parabolas. I started the class with the following prompts:
I had the students read and think about the above prompt quietly for ten minutes. I then had them have a discussion at their tables. I picked up some of the things the students were discussing:
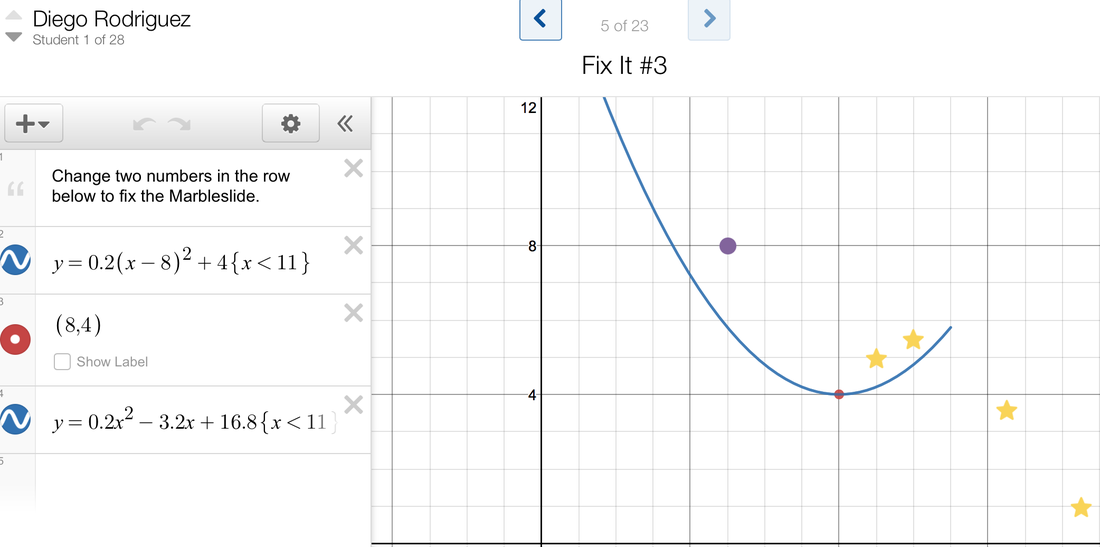
As a teacher, It's always hard not to step right in when you hear incorrect information, but I resisted, choosing to let the 'incorrect' stuff to hang out there for a bit. After about 10 minutes, I then announced: "Ok, in a moment you are going to have Watson time - a ten minute period where you can ask me anything you want. So, take a moment at your tables and come up with the burning questions that you just can't seem to answer amongst yourselves and jot them down. Take a moment...." This always sparks rich discussion as the students always want to use Watson time wisely. The funny thing is that they can ask me any questions at any point in time during class, at lunch, after school, or by email. However, when I set aside a block of time in class, they always use it as if it is an exclusive time to ask questions! Here are some of the questions that they came up with: Question 1 comes from Luke Luke: "Does intercept form mean x-intercepts or y-intercept?" Me: "What happened when you graphed it in Desmos?" Luke: "I didn't." Me: "Take a minute to graph it, jot down the intercepts, and then we can talk some more." <A couple minutes go by as I answer another question from a different student> Luke: "I graphed it. The y-intercept is 6. The x-intercept...I think there are two.....1 and 3?" Lizzy: "Yeah, there are two. Just take the opposite of the numbers in the intercept form and they are the x-intercepts." Me: "So, what do you think about your original question?" Luke:: "I forgot what it was.....ok, wait, I remember 'does intercept form mean x-intercepts or y-intercepts'. It should be called x-intercept form, it means x-intercept form." Saif: "Why do they call it that?" Me: "Who?" Saif: "The people that named it." Me: "Well, I got this name from a textbook and a website that talked about quadratics. They are mathematicians just like you - they chose a convention and it stuck." Question 2 comes from Angela Angela: "I like the vertex form because you don't have to show work to get the vertex. It's just right there. Do we have to show work on the test if we get vertex form?" Me: "Can you ask the question again but leave out 'on the test'? Angela: "Do we have to show work if we get vertex form?" Me: "Did everybody hear that question?" <a few students shake their heads no> Me: I reiterate something that I have mentioned time and time again. "Remember, this isn't just a discussion between me and the person asking the question. It's a discussion between all of us. Please repeat the question." Angela: "Do we have to show work if we get vertex form?" Me: "What do all of you think about that question?" Will: "Wait, show work when we are doing what with vertex form?" Angela: "If we have to find the vertex, and we get a quadratic in vertex form, do we have to show work to get it?" Me: "Can we have some opinions on this?" <Hands start to go up, and I give wait time> Will: <This student looks at me, but I redirect him to talk to the person that asked the question, so he does and they make eye contact with each other> "I don't think you need to show math work, the vertex is right there and that is the cool thing about that form - you can look right at it and get the vertex." Me: "How does that answer sound?" Angela: "I think it makes sense." Me: "Can we get some other thoughts on this?" Haden: "I would do the work anyway. FOIL it out and find it using the formula." Richard: "What formula?" Danielle: "Yeah, I remember a formula too. It's -b/(2a)." Me: "Okay, Danielle recommends a formula. Let's try it out. Open up your Desmos marble slides activity. You already plotted the vertex by looking at the graph and by looking at vertex form. Haden said we should use the standard form and then use the formula that Danielle is proposing. Haden, is the formula that Danielle remembers the same one that you remember?" Haden: "Yeah, I think that's it." Me: Okay, on slides 2, 4, 5, 6, 8, & 10, try the formula x = -b/(2a) and see if you get the x-coordinate of the vertex. After you try a few, go over to Haden and Danielle and see if what you are doing matches what they are doing." At this point, the class is headed in a new direction. I realize I broke my promise of "ten minutes" to ask me questions, but I think this is ok because the discussion led us this way and important points and concepts were brought up. The students work on finding the x-coordinate of the vertex for a while and many of them do not get the same value they currently see on their marble slides screen. Look at the sample marble slides screen below.  Students busy finding the vertex of a parabola using standard form. Most of the students 'knew' this material already, yet still had productive struggles on this day. Students busy finding the vertex of a parabola using standard form. Most of the students 'knew' this material already, yet still had productive struggles on this day.
Many students plugged in 3.2 instead of -3.2, which caused their value to be incorrect. They were able to self check, though, because the vertex is plotted for them on the screen. I surveyed the class and asked them how many were able to get the correct x value of the vertex using the formula. A group raised their hands, so I asked them to go to other students to check in with them to see why their values were not matching.
After a while, I ask how many of them had seen the x=-b/(2a) formula before that Haden and Danielle proposed. All but two students raised their hands. Twenty-six out of twenty eight had done this before, but there were a good number that were not successful in getting the correct x-coordinate. I then asked if any students knew how to find the y coordinate of the vertex. Several students raised their hands, and I ask them to form a group and talk over their methods, and to put any and all methods on the side board. What is interesting is that some students just plugged in the x value to the original equation to get the y-coordinate of the vertex, while other students used the formula y=-b^2/(4a) + c. At this point we have two 'competing' methods on the side board (unfortunately I didn't take pictures of this math work). I ask the class for their attention at this point: "Okay, please put your pencils down and close the laptops just so we can focus on something else. Everybody look at the side board.....can we put our pencils down and close the laptops? Let's look at the side board. Now read through the methods you see and first seek to understand what is going on." At this point the students read the side board for several minutes. I then hear chatter as they try to understand what is happening. As students start asking questions, I direct them to the students that wrote the work on the board. Those students head to the board and explain their processes. I then say, "I think it might be a good idea if we all go to slide 5 and try to get the x and y coordinate of the vertex using the methods we discussed. Why don't you try both methods to get the y coordinate and see which method you like better?" This takes a good amount of time as some students struggle through the mechanics of finding the vertex. Several students finish quickly, so I ask them to wander and help others. At this point in time, class time is about over. I realize this is not at all how I planned for things to go (I planned on having them convert between the different forms of quadratic functions), but the quality discussions and learning they were doing made it too valuable to get upset about keeping to my schedule. This is material that we were going to cover anyway, it was just moved forward based on the needs of the class. I then ended the class. "Wow, we definitely accomplished a lot today. This is not exactly what I had planned today, but I think this is what we needed at this point in time. So, for home thinking for next time, find the vertex of the equations on the rest of the slides by using the formulas proposed today. Let me know how it goes." Please check back soon for Day 5! I will be discussing the results of finding the vertex, and then move on to converting between the different forms of a quadratic. If you would like to subscribe to this blog, sign up on the upper right of this page. Happy reading!
0 Comments
|
Archives
February 2021
Categories
All
AuthorJeff Watson is a Math teacher at the University Liggett School in Grosse Pointe Woods, MI. His work as a software engineer made him realize the need for problem solvers and critical thinkers in the workplace today. Jeff believes that the secondary math classroom should be a place of critical thinking, collaborative learning, and exploration which will cultivate the problem solvers and thinkers needed today. |


 RSS Feed
RSS Feed
