|
This week in my freshmen integrated math class, the students needed to review and comprehend laws of exponents. I created a sheet with three different types of problems (see figure below). I gave the students 5 minutes to read and annotate the document. Many of the comments I saw were pretty typical: "Why isn't the three inside the radical?", "Does eight to the zero just disappear?", "What does 16^(1/4) mean exactly?" The students then discussed with their groups the various questions and comments that they originally wrote down. As I listened to the conversations, I began to realize that the understanding of the concepts and rules of exponents was not going quite as I expected. One of the students asked me, "Mr. Watson, are you going to go over these?" Translation: "Mr. Watson, are you going to go up to the front and go through each one for us?" I did not think that going to the front and lecturing was the right thing to do at that point in time. Sure, I would go up and present the rules, answers, and be proud of the clarity of math that I shared with the students, but going by the old phrase 'the person doing the talking is the person doing the learning,' I realized at that point we needed a different direction as a class. In the past, I may have given in and spent the next twenty minutes spoon-feeding the information. Instead, I tried something different.  I asked the class the following question, "Which of you understand all nine problems, and no longer have questions?" Six students joined me at the front and I called them the 'group leaders.' At that point, I used the Team Shake app on my phone to generate six teams (it literally takes a few seconds to generate the teams). I then assigned one group leader per group. I explained to the group leaders that they needed to take their group to some space in the room to ask and answer questions about the different exponent rules and examples that we were learning about. All the groups went to various places around the room - some took small white boards for their group and some gathered around the large white board. The group leaders then began to ask and answer questions to their team. The conversations began to grow and soon the groups were off and running. I was sure to listen in as the groups discussed, debated, and collaborated on the problems and ideas. It was invigorating to say the least. I was a guide for the groups - giving proper direction when the groups veered off track, answering questions at the appropriate times, and ensuring that all team members were involved in the learning. When the groups told me they were 'finished', I gave them some extra practice problems. I had the group leaders come up so we could give them a round of applause for leading the groups. After that I told everybody to go back to their home tables, and I explained to them, "In your home tables, take a few minutes and formulate any lingering questions that you may have. You are going to have a chance to ask me these questions so be sure they are good ones!" The groups discussed for a few minutes and when I could tell they were ready, I set my timer for ten minutes. I then told them "You now have 10 minutes to ask me the lingering questions. Let's do this!" There were questions, but I found that they were much deeper than I had expected. Here are some examples:
I believe that both of these questions came to light because the mechanics and rules were discussed, explored, and answered in their groups. Then they had time to ask me more of 'wonder' type questions. 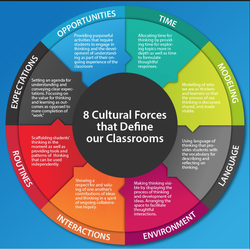 Which of the eight cultural forces were leveraged during this class period? Here is one view: Expectations: Student independence was actively cultivated by having them work in groups with group leaders and to be actively engaged with each other. The students directed most of the activity. Language: During the lesson, I tried to give specific action-oriented feedback, such as, "I like how you explained the fractional exponent rule here and the example that you used" and "This was a clever way to explain this to your group - it seemed like they really grasped the concept." Time: I really tried to monitor the amount of time that I talked during this lesson - it was limited to small chunks of time. The most that I was at the front talking at the class was the 10 minute session near the end. Interactions: Groups acted independently and many times I just listened in to hear their thinking. Many students challenged ideas, not the people pitching the ideas. Opportunities: Students got the opportunity to direct their own learning in their groups. The group leaders led the way, but all group members were allowed to questions and direct what was happening. In a previous article, I spoke of a "lawn" math classroom vs. a "ravine" math classroom. I believe that this class period was definitely exploring the "ravine!"
0 Comments
At the 2017 Project Zero classroom in Cambridge, MA, David Perkins described a setting in which he was sitting on a well-manicured, perfectly green lawn, while a few feet away at the edge there existed a colorful, wild, interesting ravine, full of life and questions. He asked the participants: 'Is your classroom a lawn - well manicured, predictable, and neat, or is it a ravine - wild, messy, with organized chaos?'  This got me thinking about my own classroom, of course, and how for many years, my room primarily fit the description of a well-manicured 'lawn.' But what does a 'lawn' math classroom look like? What are its characteristics? I came up with a short list:
After thinking about this for a while, I remember an example math classroom from "Creating Cultures of Thinking: The 8 Forces We Must Master to Truly Transform Our Schools" by Dr. Ron Ritchhart, a member of the Project Zero team at Harvard University. In it, Dr. Ritchhart describes a math classroom in which he "had a hard time finding moments when students were truly engaged in any thinking" (Ritchhart, p. 39). The teacher was described as very personable, and was reliably consistent with her students, but that it seemed the students "made an internal calculation regarding how much attention needed to be paid to complete the homework successfully or prepare for the looming test" (Ritchhart, p. 40). This classroom seems to be primarily a 'lawn' classroom, with little, if any, ravine characteristics.  Now, to be clear, there is nothing inherently 'wrong' with a having a 'lawn' classroom some of the time, perhaps for part of a class period, or for an entire class period. There needs to be a good balance. The issue, in my opinion, is when a math classroom becomes a lawn day after day, and week after week, because this causes the teacher to do a majority of the critical thinking and the rich opportunities for student learning are lost. This idea of lawn versus ravine ties nicely with the eight cultural forces that make up the Cultures of Thinking (CoT) framework: expectations, language, time, modeling, opportunities, interactions, routines, and environment. If properly leveraged, the eight cultural forces could create a classroom culture that mimics the 'ravine', with some 'lawn'. However, if left to fester and not leveraged properly, the classroom could become primary a 'lawn', with little 'ravine': predictable, well-managed, but lacking the deep thought necessary for 21st century learning. So, how do the eight cultural forces 'look' in a math classroom that is primarily a 'lawn'? Let's take a look at each force: Expectations: Many things are expected of students in this type of classroom. The teacher may say things like:
Language: The key language moves to create a culture of thinking that Ritchhart describes are the language of thinking, community, identity, initiative, mindfulness, praise and feedback, and listening. In a 'lawn' classroom, some of these key language moves may not exist at all, or may be counter-productive to a culture of thinking. For example, if a teacher is continuously the sage and provider of information in a classroom, then students may never hear the language of community and identity. Furthermore, the language of praise and feedback may strictly be a language of praise without a language of feedback. Generic praise comments might include 'good job', 'great', 'brilliant', instead of action-oriented feedback such as 'I like how you completed the square here - I have not seen that before' or 'your graphs here are very detailed and it took very little time for me to get a clear picture of what is happening.' Time: In a lawn math classroom, time may be used very well and there may not be a second to spare, but the time spent may not be on critical thinking. For example, if a lot of time is spent in lecture or sit-and-get mode, then time is allocated and used, but students are merely scribes at that point, with little or no thinking being accomplished. If this is the case, there might not be enough time for students to process ideas. As a general rule, a teacher should not talk for more than ten minutes at a time in order to give students processing time. Modeling: The cultural force of modeling as described by Ritchhhart is the teacher as a role model of learning and thinking; in a lawn classroom the modeling may be predominantly instructional modeling which consists of the teacher showing techniques and methods to 'show the work' and 'get the right answer.' As a role model of learning, the teacher should be modeling how to take risks and reflect on the learning. It's ok for a math teacher to say, 'I'm not sure why dividing by 5 stretches the graph - I need to look into that more. It does seem like the graph should shrink. Why don't we do some research and we can talk about it next time and coordinate our ideas?' Opportunities: What opportunities are 'lawn' math classrooms providing for students? Ritchhart states that 'opportunities that teachers create are the prime vehicles for propelling learning in classrooms.' In 'lawn' math classrooms, the opportunities for rich thinking in which the student examines, notices, observes, identifies, uncovers complexities, and captures the essence of something may be limited. If a math classroom consists of homework check followed by direct instruction, day in and day out, then it is very possible that a student does not think at all, outside of the elementary tasks of 'paying attention' and 'taking notes.' As a math teacher, do you take quality time when planning to ensure that your students have rich opportunities? 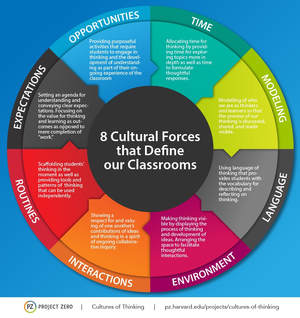 Interactions: A 'lawn' math classroom may consist of a lot of QRE interactions, which stands for Question-Respond-Evaluate - the teacher asks a question, a student responds, then the teacher evaluates that answer. This results in a 'Ping-Pong match back and forth between the teacher and a single student, leaving much of the class out of the interaction' (Ritchhart, p. 212-13). The interactions that should be fostered are ones where the students are pushed to reason and think beyond a simple answer. Routines: A 'lawn' math classroom may be littered with procedural routines, for example:
 Environment: Take a look at the image created by Thomas Murray ([email protected]) on the left. Does this look familiar? Not much has changed if you compare the class from 1916 to the one from 2016, yet the world around us has changed in so many ways. In many math classrooms, desks in rows are still a reality. Is there a place for this? Sure there is, perhaps during tests or at a time where a mathematical procedure needs to be shown. However, this should not be the primary setup; it should be changed to allow students to have richer learning opportunities, interactions, collaborations, and discussions. So, what is a 'ravine', and what do the eight forces 'look' like in that type of classroom? Stay tuned as I will look at that in the next blog post! |
Archives
February 2021
Categories
All
AuthorJeff Watson is a Math teacher at the University Liggett School in Grosse Pointe Woods, MI. His work as a software engineer made him realize the need for problem solvers and critical thinkers in the workplace today. Jeff believes that the secondary math classroom should be a place of critical thinking, collaborative learning, and exploration which will cultivate the problem solvers and thinkers needed today. |

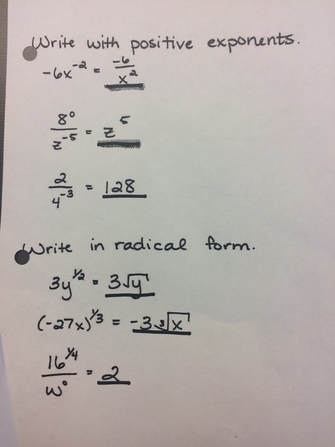



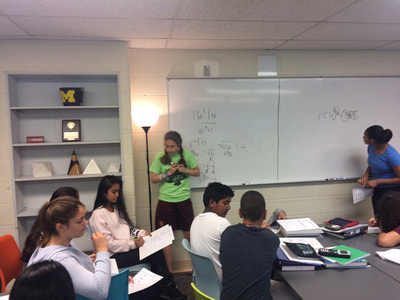



 RSS Feed
RSS Feed
