Quadratics Day 1: Planning an entire unit with Cultures of Thinking in mind

 

This blog is re-posted from November, 2017.
I have been teaching for quite a while and have taught units on quadratics more times than I can count.  The concepts of vertex, line of symmetry, factoring, quadratic formula, and intercepts were frequently discussed, often times in more than one class.  More often than not, when I was a 'section' teacher, I followed the current textbook's recipe on how to do this.  The current textbook I am working with lays it out like this: 

• Section 1: Graphing quadratic functions
• Section 2: Translating parabolas
• Section 3: Solving equations using square roots
• Section 4: Solving equations using factoring
• Section 5: The quadratic formula
• Section 6: The discriminant and complex numbers
• Section 7: Quadratic systems

The current class that I am covering this unit with is a class of freshmen; the last time I taught this particular class was three years ago and I covered it section by section.  The mode of teaching was mainly lecture, with students practicing problems, mainly on their own.  My classroom at the time was organized in rows, and the students had homework from the textbook each day that they had my class.  

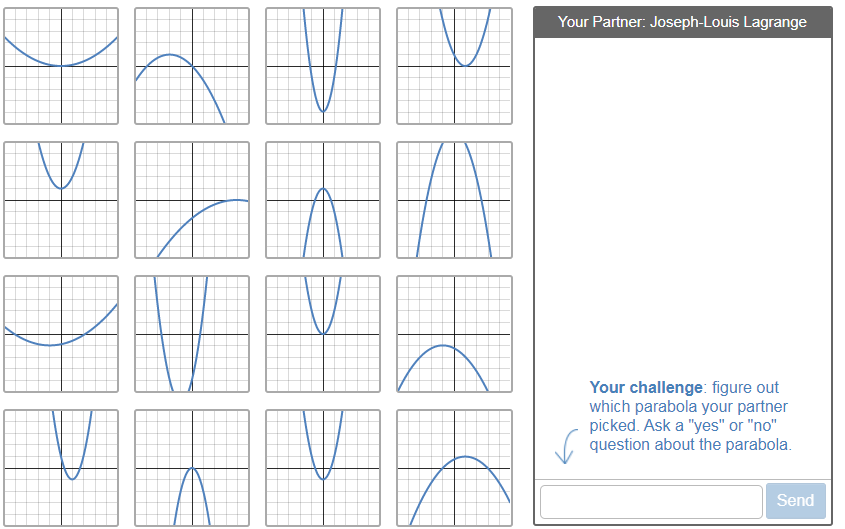
Many times at the start of this unit I would show the students how to graph basic parabolas - I would define the key items such as the vertex, line of symmetry, and intercepts, and then graph them.  The students would copy what I was doing and then do homework problems essentially replicating this behavior.  The students' thinking only went as far as the rote mechanics they were employing when finding the key items.

As I approached this chapter this year, I was thinking about how to organize the lessons to best suit the students.  It then led me to the question, 'How can I organize this unit so that I am able to leverage the 8 cultural forces described in 'Cultures of Thinking: The 8 Forces We Must Master to Truly Transform Our Schools' by Ron Ritchhart, in a way that helps students the most?'

I have organized this blog post in to several days.  Today I will cover day 1, with other days following soon.

Day 1: Polygraph parabolas
On this day, I wanted the students to speak the language of parabolas.  Our foreign language teachers tell me that the best way for students to learn about the language is to speak it - so it seemed reasonable that the best way for students to begin to learn about parabolas is to speak about them.  I decided to start the unit by using the "Polygraph Parabolas" activity on www.teacher.desmos.com.  All the students need a computer and sign in to the activity after receiving a special code that Desmos generates.  I decided to sign in as well so I could do the activity with them.  When everybody signs in, Desmos pairs everybody up randomly. 

​The opening screen of the activity looks like this:

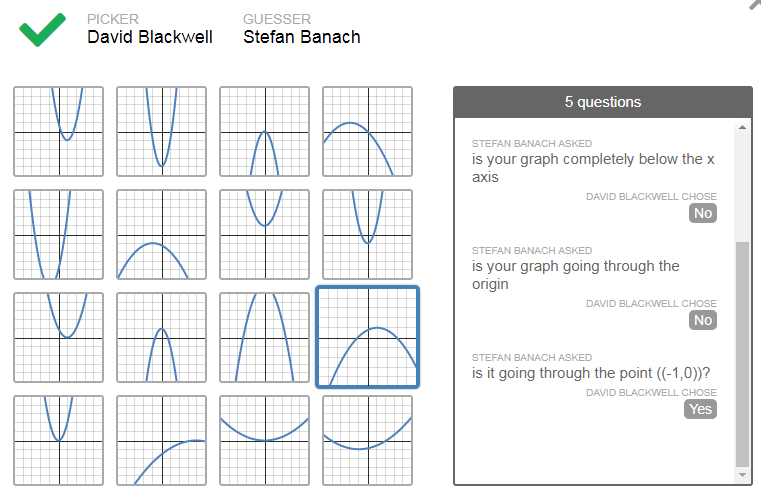
Student 1 of the pair chooses their 'favorite' parabola, and then Student 2 of the pair asks questions to try to figure out which parabola that Student 1 picked.  Student 2 has to ask yes-no questions, and then Student 1 answers them.  Take a look at the sample interactions below.  One nice feature of desmos activities is you can anonymize the names so the students' real identities are hidden:

Students engaged in 'Desmos Polygraph: Parabolas'

   As you can see from the above interactions, the students must use mathematical language in order to communicate with each other.  I used this in more than one block, and the activity would start out very quiet as the students communicated via the computer as they typed in and answered their questions (much like they interact when texting each other).  However, in every class, as time went on, the students began to interact with each other with live conversations.  It was really awesome to see that unfold.  I would hear things like "what do you mean by ...", "when you say the graph is positive, what do you mean exactly",  and "when you say minimum, do you mean the vertex or another point?"  The best part about this computer interaction and live interaction is the students were communicating with each other with mathematical language.  At the beginning of the activity, the language was imprecise but as time went on it became more detailed and mathematically correct.  The best part of it was when the students used their own language to start with, such as "x-axis crossing points" and "bottom point", and then to see it slowly transform into terms such as "intercepts" and "vertex."
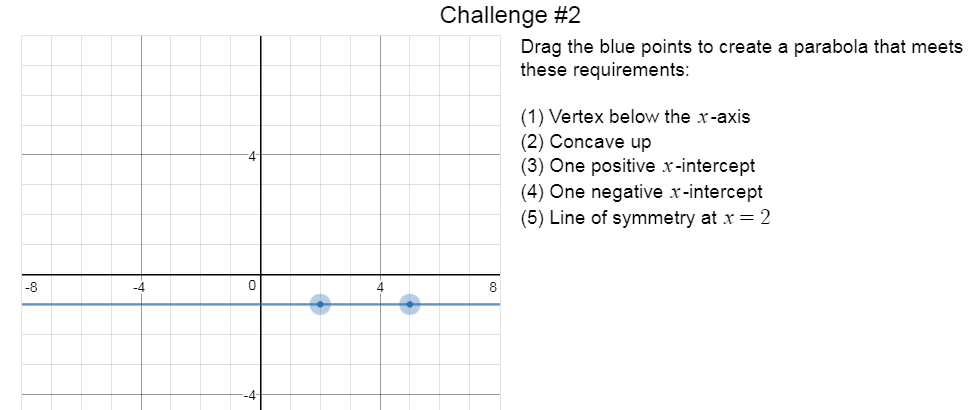
       I let the students play this activity for about 30 minutes.  After this, there is another desmos activity related to this called "Polygraph parabolas, part II" that I let the students explore.  This activity takes some of the imprecise language, such as 'turning point', 'smile', and 'touches the middle line twice' into language such as 'vertex', 'concave up', and 'intercepts.'  At the end of this activity, the students are asked to create parabolas with certain characteristics.  Here is an example:

---

 There are many cultural forces at play during this day in math class.  Here is a look at some of them:
1. Language: The language of community is very evident as the students are creating the vocabulary that is used to communicate about parabolas.  Often times during the course of the polygraph activity, students ask me 'is this the way to say it' or 'is this right?'  My response is always 'are you able to communicate with your partner effectively with the words you are choosing?  Perhaps you should talk with them and get the vocabulary ironed out.  Later in the week we will see what other mathematicians have used to communicate, and we will also talk about why they might use the language they use.'  This allows the students to have a sense of community and to see that math is not something that is defined outside of our classroom - rather it is something we develop as a community of mathematicians.
2. Modeling: By participating in the activity with the students, I tried to model that I am a learner with them and that I am not the sage of parabola vocabulary.  I wanted them to see me as a role model instead of an exemplar.  As they worked through questions about parabolas, I noticed the students leaning on each other to make sense of what was going on - they slowly became independent and confident in talking about parabolas.  If I would have used transmission of knowledge as the mode of teaching on this day, students would have missed out on this rich activity and would have seen me as an exemplar instead of taking control of their quadratic vocabulary.
3.  Interactions: It goes without saying that the Interactions were a big part of this day.  Most students interacted with over half the class because when one partnership ends, desmos automatically matches the students up with somebody else that is waiting.  As I said earlier, what started out as virtual interactions slowly turned into live interactions as the students were trying to sort out their thinking.  
4. Opportunities: The best part about providing this opportunity for the students was that it was a low threshold opportunity - all students could participate.  Some of the students already knew the 'perfect' parabola vocabulary, while those that didn't improvised by using words that made the most sense to them.  Some students were using phrases such as 'bowl shaped', or 'smile' to describe a certain parabola.  I think that was great.  If I would have just told them to say 'concave up' instead of 'smile' it would have been my words and not their own.
5. Environment: The environment on this day was one of organized chaos.  There was structure for sure as the students were at their computers and playing a polygraph game, but the overall atmosphere was one of curiosity, thinking, and laughter as the students tried to communicate with each other about a topic that was new to many of them.

In upcoming posts, I will describe how to leverage Cultures of Thinking with the rest of the quadratics chapter. 
​
Later this week, I will cover what happened on Day 2: Marbleslides: Mapping the shape of a parabola to the equation that generates it.  

Please visit again!