Quadratics Day 2: Planning an entire unit with Cultures of Thinking in mind

 

As I contemplated what to have the students do after their 'Polygraph: Parabolas' activity on Day 1 (see Day 1 post here), I needed to take inventory of what the students learned up to this point.  I tried making a list, and then realized that it would be better if the students made the list instead.  This led me to the new thinking routine, the '+1 Routine', under development for the Making Thinking Visible 2.0 book, which is under development by Ron Ritchhart and Mark Church of the Project Zero team at Harvard University.

The routine goes something like this:

1. ​Recall: In 2-3 minutes and working individually, each learner generates a list of key ideas that they remember about a topic.
2. Add (+) 1: Learners pass their papers to the right.  Taking 1-2 minutes, each student reads through the list in front of him/her and adds one new thing to the list.  The addition might be an elaboration (adding a detail), a new point (adding something that was missing), or a connection (adding a relationship between ideas).  REPEAT this process at least two times.
3. Review: Return the papers back to the original owner.  Learners read through and review all the additions that have been made on their sheets.  At the same time, they may add any ideas they have picked up from reading other's sheets that they thought were worthwhile.

The reason I decided to use this routine is because I wanted to see what key ideas the students remembered from the Polygraph activity, and how well they committed them to memory.  I had the students close their laptops and put away their source material.  I gathered the students in groups of five for the routine and I handed each student in the group a different colored pencil.  The routine went something like this:

• Me: 'Okay so each of you take out a piece of paper.  I know you get to work collaboratively a lot in this class, but for right now I want to know only what is in your mind.  So, when I say 'go', I want you to write down any key ideas about parabolas that you can remember.  Remember, this is your own work.  You will have exactly two minutes.  Go...'
• The students wrote their lists for two minutes.  Each student in the group used a different color so they could easily see who was writing each part.  
• After the 2 minutes passed, I said 'Now, take your list and pass it clockwise.  Read the list.'  I paused here and gave them time to read.  Then I said 'please add one new thing to the list.'  After a minute, a student said to me, 'Mr. Watson, I added a new item, but what if I saw something wrong with what is currently there?'  This caught me by surprise because I didn't think about this.  So, I had them pass the papers again in the clockwise direction, and gave a slightly different direction this time.  I said, 'This time, read the list, and then either correct something that is there, or add something new to the list.
• This continued for five iterations before the papers went back to the original owner.  I then had the students read their original paper.  I told the students to chat with their group about what they had read.  Since the writing was in different colors I told them to chat with the person with that color if they had questions or comments.  Here is some of what I overhead the students saying to each other:
  • ​"Wait, this isn't incorrect?  Why did you correct this?"
  • "I'm not sure what you meant by 'middle number.'  Can you explain this?"
  • "Completing the square.  What is that?  Did we do that the other day?"
  • "I still don't understand 'line of symmetry.'  Somebody wrote x equals negative b over 2a.  That didn't make sense the other day either."
• This sparked rich interactions between the students.  I'm glad that we spent the time to do this as it brought their current thoughts about parabolas alive on the paper.  Some students wrote items that they had learned in middle school, but were not yet discussed this year.  In the past, I would tell students 'not' to discuss those things because we hadn't 'covered' them yet.  Now, I encourage all prior knowledge and want the students to share it.

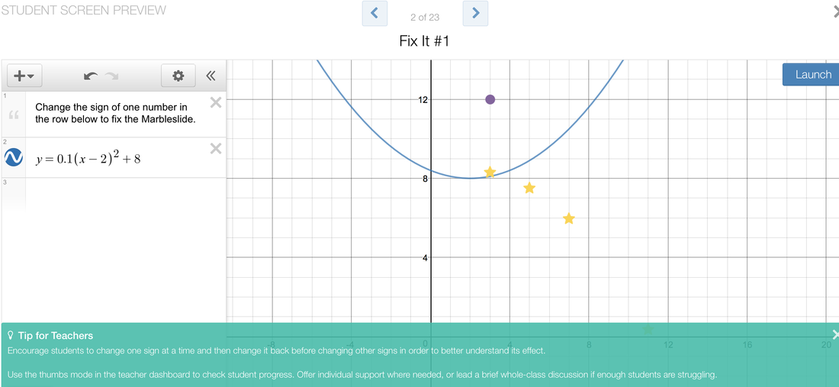
I had one person from each group read their list, and then I said the word 'popcorn.'  This is a signal to students that I am looking for a comment or feedback on what was just read.  The student that did the reading then called on a person of their choice to share their thoughts.
The +1 Routine provided a great recap of the previous day's lesson, and sparked more of the vocabulary that I wanted the students to continue to use.  

Where did we go from here?  The polygraph activity on the previous day involved only graphs of parabolas - the students did not see the corresponding equations that generated those parabolas.  It seemed logical to me that they should spend time associating parabolas with the equations that generate them.  

This led me to the Desmos Marbleslides parabola activity.  As you can see from the sample screen below, in this activity the students have to use the vertex form of a parabola in order to 'catch' stars with marbles rolling along the parabolic curve.  They are given an initial curve, and then have to change the values of a, h, and k in order to get the parabola in a certain shape to catch all the stars.  Once they feel confident that their shape will work, the students hit the "Launch" button which releases the marbles (the first marble is the purple dot) which 'hit' the stars.  Once all the stars are hit, the student gets to move on to the next screen which is a new curve and a new set of stars.   

---

Sample Marbleslides screen

Students working on the Desmos marble slides activity.

After the students got a feel for the first couple of slides (teachers are able to pace the activity so students can only work on certain slides at one time), I paused the activity to give a new set of directions.  I had them each take  out a piece of paper and explained that they would be documenting their thinking as they went along.  I felt it was important for them to do some additional thinking about what they were doing with desmos in this activity and to write it down.  I have students record all of their desmos activities so they can go back to them later, but I also wanted to see some documentation of their thinking.  I wrote the general form of the vertex form on the board, and proposed the following questions as they were going through the activity:

• What effect do the values of a, h, & k have on the graph of y = a(x-h)^2+k?
• Identify the vertex on slides 2,4,5,6,8,10 in the Marbleslides desmos activity.  Plot the vertex in desmos.  How does the vertex relate to the vertex form of the equation on each slide?

​
These prompts gave the students some things to think about as they changed the graphs of the quadratic equations.  I gave the them time to complete more slides and think about the above prompts, and then explained that their home thinking due the next class was to finish the marble slides activity, and to answer the above two prompts.

In the Day 3 post, I will discuss how the students converted between vertex form and standard form, and how they used Desmos to 'check' if their conversions were correct.

​Stay tuned!

---