 Microlab Protocol Microlab Protocol
The home thinking that the students had to do at the end of day 2 was the following:
The students turned in their documentation of their thinking as they walked in to class. I looked at it briefly, checked that they completed it, and then handed it back to them. I used the "Team Shake" app on my phone to generate groups of 3. I then asked them to run through the MicroLab protocol to discuss their thoughts on the values of a, h, & k (If you are not familiar with the MicroLab protocol Visible Thinking routine, see the image below). I displayed the slide to the right in class and did not have to explain too much because we had used it before. I just reminded them that as each person is talking, the other two needed to listen only. We ran through the protocol, and then I asked the groups of three to have an open discussion. After this I had the students go back to their home tables and to verify their thinking about the values a, h, & k, and then we had a class discussion about these values. As a final check for understanding, I had the students close their laptops and answer the following questions: I circulated around the class and looked over their shoulders at their responses. After about ten minutes I told them to open up Desmos.com to check their answers. I circulated and the students entered the 5 equations in Desmos to check the 'width' of the graphs to verify if they had them in the right order. Some of them had questions, which I addressed and overall the problem went well. The second question, though, was a different story. I thought it was going to go quickly. I thought to myself, "If you take 3x^2 and shift it left 4 units, you obviously get 3(x+4)^2 and you go on your way." The students had real trouble with this. Many of them wanted to add an x term and a constant term to get the graph to shift. Most students shifted the graph to the left, but not by 4 units. Some of them shifted it left 4, but then it moved up or down as well. I was puzzled as I thought since they had played with the equation y=a(x-h)^2+k in desmos, and tried different values, they would understand the connection. As I questioned more students and tried to get the big picture it was clear to me that they did not see y=3x^2 as possibly in vertex form. So, I wrote the equation on the board as y = 3(x-0)^2+0. Bingo! Lights on! They caught it immediately and went on their way. One of them said to me, "But I thought y = 3x^2 was in standard form?" Another responded to her saying, "It looks like we have an example that sort of fits both forms." Still another said, "What is standard form?" I laughed out loud, not at the kids of course. I explained to him that this was one lesson that did not go as I had scripted, but it was necessary because that is what the class needed.
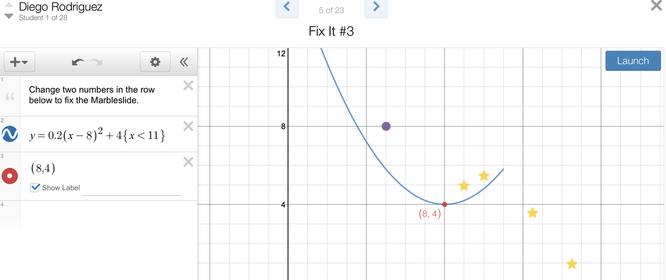
After we got this squared away, I had them open the Marbleslides activity (they can log in so it is saved - see the sample screen below). I walked around and checked if they had plotted the vertex on their parabolas and they had, and asked them how they found the vertex. One student said, "I just looked at the graph and knew where the vertex was at and made a best guess on what the coordinates would be." I asked how many had did it this way, I about ten of them raised their hands. I said, "How did the rest of you do it?" One student chimed in, "I just looked at the vertex form, took the h and the opposite of k, and knew that that was my vertex. Then I plotted it."
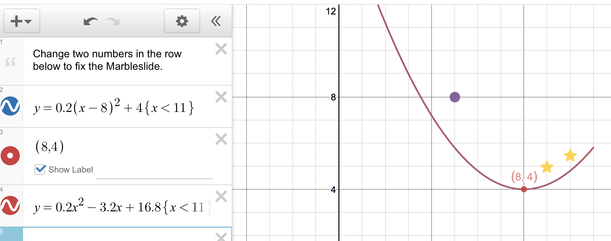
I said, "It sounds like we have two methods: one is looking at the graph, the other is to look at the equation. Which is better?" A student said, "I like looking at the graph and making a best guess. I'm visual" while another said that using the equation to get the vertex was more exact. I said that sometimes in math we have several methods to do things. However, I did mention that if they didn't have the graph in front of them to look at, that they needed to be able to use the equation exclusively to find the vertex. At this point I projected the marble slide screen shown above for the whole class to see. I then typed in a different form of the equation that was already there, but this time I put it in standard form (see picture below). I asked the kids what was happening here, and I made sure to give proper wait time. Here are a few responses:
I asked the class how many of them had familiarity with FOIL. Most of them raised their hands but there were some that did not. I wrote the conversion on a sheet of paper and when I was finished, I projected it on the document camera. I then asked them to take a couple minutes at their tables to read what I had written and to discuss it. I purposely put a mistake just to see if they would catch it. The discussions were rich as the students that remembered FOIL were explaining it the students that either never saw it before or forgot about it. The one comment that I took away from this was from a student that said, "I knew how to do FOIL, but I never knew why I was doing it." I then gave them their thinking for the rest of the class period and for home thinking for that evening:
Go to slides 2, 4, 5, 6, 8, and 10 in the marble slides activity and convert your equations from vertex form to standard form. Do the conversions on paper so you can get the mechanics down, and then plot your answer on the marble slides screens to make sure it completely matches the graph that is already there.
0 Comments
Your comment will be posted after it is approved.
Leave a Reply. |
Archives
February 2021
Categories
All
AuthorJeff Watson is a Math teacher at the University Liggett School in Grosse Pointe Woods, MI. His work as a software engineer made him realize the need for problem solvers and critical thinkers in the workplace today. Jeff believes that the secondary math classroom should be a place of critical thinking, collaborative learning, and exploration which will cultivate the problem solvers and thinkers needed today. |

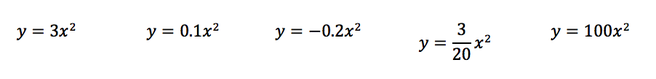
 RSS Feed
RSS Feed
