As I contemplated what to have the students do after their 'Polygraph: Parabolas' activity on Day 1 (see Day 1 post here), I needed to take inventory of what the students learned up to this point. I tried making a list, and then realized that it would be better if the students made the list instead. This led me to the new thinking routine, the '+1 Routine', under development for the Making Thinking Visible 2.0 book, which is under development by Ron Ritchhart and Mark Church of the Project Zero team at Harvard University.
The routine goes something like this:
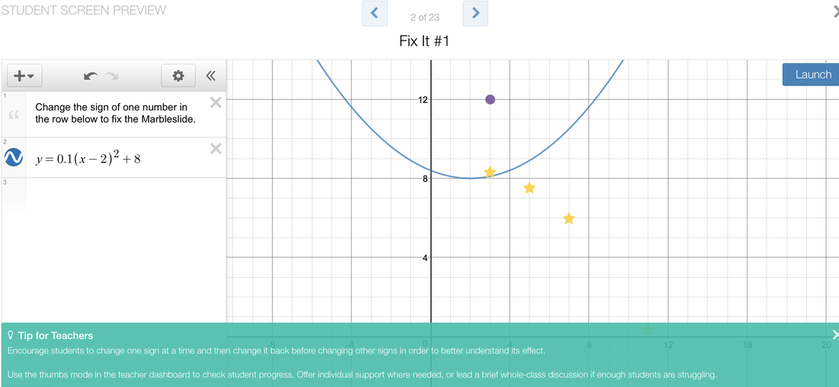
I had one person from each group read their list, and then I said the word 'popcorn.' This is a signal to students that I am looking for a comment or feedback on what was just read. The student that did the reading then called on a person of their choice to share their thoughts. The +1 Routine provided a great recap of the previous day's lesson, and sparked more of the vocabulary that I wanted the students to continue to use. Where did we go from here? The polygraph activity on the previous day involved only graphs of parabolas - the students did not see the corresponding equations that generated those parabolas. It seemed logical to me that they should spend time associating parabolas with the equations that generate them. This led me to the Desmos Marbleslides parabola activity. As you can see from the sample screen below, in this activity the students have to use the vertex form of a parabola in order to 'catch' stars with marbles rolling along the parabolic curve. They are given an initial curve, and then have to change the values of a, h, and k in order to get the parabola in a certain shape to catch all the stars. Once they feel confident that their shape will work, the students hit the "Launch" button which releases the marbles (the first marble is the purple dot) which 'hit' the stars. Once all the stars are hit, the student gets to move on to the next screen which is a new curve and a new set of stars.  Students working on the Desmos marble slides activity. Students working on the Desmos marble slides activity.
After the students got a feel for the first couple of slides (teachers are able to pace the activity so students can only work on certain slides at one time), I paused the activity to give a new set of directions. I had them each take out a piece of paper and explained that they would be documenting their thinking as they went along. I felt it was important for them to do some additional thinking about what they were doing with desmos in this activity and to write it down. I have students record all of their desmos activities so they can go back to them later, but I also wanted to see some documentation of their thinking. I wrote the general form of the vertex form on the board, and proposed the following questions as they were going through the activity:
These prompts gave the students some things to think about as they changed the graphs of the quadratic equations. I gave the them time to complete more slides and think about the above prompts, and then explained that their home thinking due the next class was to finish the marble slides activity, and to answer the above two prompts. In the Day 3 post, I will discuss how the students converted between vertex form and standard form, and how they used Desmos to 'check' if their conversions were correct. Stay tuned!
0 Comments
Your comment will be posted after it is approved.
Leave a Reply. |
Archives
February 2021
Categories
All
AuthorJeff Watson is a Math teacher at the International Academy East in Troy, MI. His work as a software engineer made him realize the need for problem solvers and critical thinkers in the workplace today. Jeff believes that the secondary math classroom should be a place of critical thinking, collaborative learning, and exploration which will cultivate the problem solvers and thinkers needed today. |

 RSS Feed
RSS Feed
