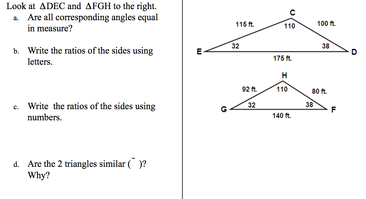
 Figure 1 Figure 1 Recently we started a lesson on similar triangles. I thought a lot about what to have the kids do, and a small part of me (very small) wanted to 'direct teach' the lesson to save time - we are behind, after all, and if I just told them what similar triangles were and what to do with them we could move on to the next lesson. In the past, I would typically give them scripted notes that had a set of similar triangles, such as the example in figure 1. I would explain what similar triangles were, and how to find different things about them, such as angle measures and/or side lengths. The students would typically do well with this and then we could say that we had 'learned' similar triangles. This year I wanted to provide a richer opportunity for them. I put up the following directions:
I purposely made the direction vague. Some students asked me what similar triangles were, but I pushed it back to them to use their resources, such as their phone, computer, or textbook, to figure it out. Some students also asked what I meant by a 'set' of similar triangles. I asked them to look up that word as well and then decide what to do. I had to laugh because some students just really needed me to tell them 'how many' triangles they needed to make. I did not want to tell them because I did not want to give them a threshold at which to stop learning. As time passed, many students were using their protractors to create two triangles that had the same angle measures. Two seemed to be the most popular number of triangles. There were a lot of struggles going on as measurements were being made and sides were being measured. Some students used a lot of paper, while others used a sheet or two. With about ten minutes to go in the block, two of my students, Filip and Haden, asked me to come and look at their set. I walked over to their desk and this is what I saw: Needless to say, I was floored! The expectation in my head was to see two triangles that were created using straight edges and rulers. I of course inquired about what had happened and what led them to this result, and I found out what actually happened: they used one sheet of paper and created thirteen (or so) triangles in about 5 minutes. All of the triangles were similar, but the beauty of it was that they did it by folding the paper - rulers and protractors were not needed (one is shown in the picture, but it wasn't used). The best part was that I was going to demo to the whole class how to 'quickly' create two similar triangles (by overlaying them on each other), and instead I had these two students demonstrate a much more powerful demonstration.
I was really thankful afterwards that I didn't give in to the urge to instruct directly because this opportunity would have been completely lost. Instead, it was gained, and was a nice lead in for the next class, as I had Haden and Filip lead the class on how to construct so many similar triangles in such a short time.
0 Comments
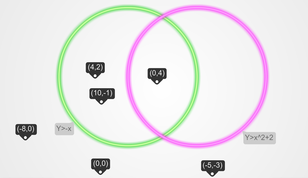
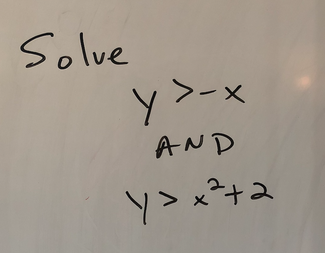 One of the concepts we have been studying in my freshmen math class is solving systems of inequalities, such as the system seen below. In the past, the lesson would go something like this: 1) I would model how to draw each curve in the system. 2) I would draw dashed or solid lines and explain why they were dashed or solid. 3) I would shade the appropriate region and explain how to determine this. 4) I would ask if there were any questions and would address them with each student directly. 5) I would give the students a different, but very similar example to do and monitor their progress. At the end of this lesson, students could claim that they knew how to solve a system of inequalities by simply replicating the steps that I gave them in class. I really wouldn't allow much variation in the procedure - I had the math degree, after all, and I told the students that we all need to be on the same page as far as the 'right' way to do this procedure. This approach made me think of some of the belief sets that are discussed in the Expectations chapter in "Creating Cultures of Thinking: The 8 Forces We Must Master to Truly Transform Our Schools." The belief sets, which are outlined as natural tensions, that came to mind for this lesson are focusing on the learning vs. the work, teaching for understanding vs. knowledge, and encouraging deep vs. surface learning. As I reflected on the way that I used to teach this, I imagined that the students had the knowledge of how to graph an inequality, that they knew how to complete the work required (especially given the fact that I would assign a bunch of these types of problems for homework), and they at least had developed learning on a surface level. Obviously, these are not bad things in and of themselves, but how could we develop a deep level understanding of learning that was meaningful? I attempted to do this with the following lesson. I started class by displaying the problem above. I asked them to draw the solution on their desk (their desks are white boards) using whatever prior knowledge they could remember. There were definitely some cob webs as the students tried to remember what they had learned previously. A lot of discussion ensued: 'how do you draw this parabola?', 'I remember having to use dashed lines - do we do that here?', 'is shading a thing with these problems?', 'I think we shade everything, don't we?' It was tempting at this point to walk around and quickly check these for the kids and tell them right or wrong. It certainly would have made the lesson go faster, but in trying to foster independence I tried something different. I had the students check in with their group members (the students are in groups of 4) to compare and contrast their graphs and to come to an agreement on what was correct. Then, they had to erase the four graphs and create one that the group could agree on and draw that one rendition. In my classroom there are eight groups of four, so at the end of this there were eight graphs total. Each group collaborated, questioned, erased, shaded, and played until they were happy with their final product. I then had the groups rotate around the classroom. Each group was instructed to carry one marker and to 'annotate' the final product at each group. If they saw something that somebody else had already written, they had to put a star next to it. After a slew of rotations around the class, everybody came back to their home group and were able to see the comments, suggestions, fixes and feedback that were left at their table. I gave them a few minutes to digest everything that they saw. 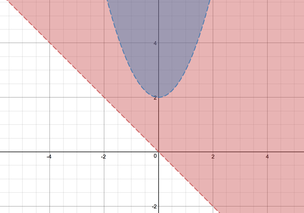 I then put up the following drawing using desmos. I asked them to compare what they had with what they saw from desmos and to write down what they were wondering about. Here are some samples: - is the blue and the red region necessary? - is the white region part of the answer? - i still don't understand the dashed lines - is desmos right or am I right? I asked the class "Which region is the correct region? Is it the blue, the red, both of these, or the white? Many students chose blue, some chose red, while some chose both. I called their attention to the fact that in the original system, the word "AND" was used, which in math means intersection. 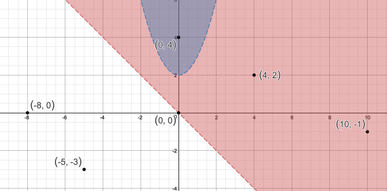 I then showed them the same graph in desmos, except now with some points plotted in the different regions. I asked students that were comfortable to go and plot more points in the various regions, so they slowly went up and put more points on the screen. Instead of asking which color regions were the solutions, I asked which points were the solutions to this problem. Many students mentioned the point (0,4), as well as others that were in the blue, but some still called out points (4,2), and (10,-1) in the red region.  At this point, I displayed the following Venn diagram on the board. I asked them to draw this Venn Diagram on their desk and to place the coordinate points in the appropriate places in the Venn diagram. They had been exposed to Venn diagrams in the past, and for the most part knew that the AND part was the portion in the middle of the diagram. They slowly started placing points in various spots on the diagram, and were trying to figure exactly where the coordinates would fit. However, the most fun occurred when I asked each group to create their own systems. They could include any functions that they were familiar with as long as they had general knowledge of how to draw them. This was fun to see develop as some groups created a system with a line and quadratic (just like mine!) and I told them to go back to the drawing board and make it a bit more interesting. One group brainstormed a list of the functions they were familiar with before choosing. Still another group picked three functions instead of two. Regardless, the kids came up with much better examples and insight than I could have, and it certainly was much more rich than me just handing them a system to solve!
The eight new systems served as a springboard for more practice. I gave the students a choice on which systems they wanted to tackle, and when they wanted to tackle them, whether it be at home, during class, or after school. This video features a presentation by student Christina Thymalil who originally researched this topic for a Theory of Knowledge (IB curriculum) class. In her presentation she focuses on how core classes such as math and science tend to enable teaching practices such as spoon feeding and idle note taking. But, new ideas based on the book "Cultures of Thinking" by Ron Ritchhart, depict several methods on how incorporating different cultures in the classroom can enable any class to become a medium of creativity and independent thinking. Over the past couple of weeks I have been posting about the quadratic unit that we are covering in my freshmen math class. Today I am going to deviate from that a bit to talk about a lesson that occurred today. The first part of the next unit is using exponent rules to simplify expressions. There are a lot of mechanics involved, and the practice problems can get quite tedious. Lately I have been telling my freshmen that teachers are like personal trainers. I gave them this scenario: imagine you go to the gym with your personal trainer. For an hour you watch your trainer run 5 miles, then afterwards you watch them lift weights. At the end, you leave the gym and say that you "worked out." Ridiculous right? The personal trainer should show you some exercises and guide you to best practices, but at some point you need to perform those exercises and routines yourself, and go through the sweat and tears. Teaching and learning is much like that. The teacher can guide and show certain things, but the students must perform the exercises and go through the sweat and tears much the same way as in the gym. I thought to myself: 'How can I guide my students through these exponent rules while giving them the opportunity to go through the sweat and tears necessary to deepen their learning?'  First, I created examples for them and handed them out. Above is one of the examples that I gave the students. You can download the full worksheets here. As you can see, the worksheet isn't anything special - it is something that I've more or less handed out every year. I then organized the class in to six groups using the Team Shake app. You can see the organization of the teams on the right. After the class re-organized themselves in teams, I said the following: "Okay, all of you are in your teams. Team 1 is responsible for Example 1 in the packet I gave you, Team 2 is responsible for Example 2, and so forth. Your team needs to think about the problems in your example and talk together to determine how to do them. Perhaps some of you have seen this before and you can start the group in that direction, or maybe you want to go to www.wolframalpha.com, type in your question, see the answer, and then work backwards. As always, you can ask me well thought out questions. In addition, each team gets one "spoon feed" - I will work out ONE example for you if your group requests it. I won't tell you what I am doing, though, it will just be the work and process written on a small white board. Okay - enjoy!" I left the team arrangements showing on the screen. The students went off in their teams and began their problem set. Here are the things I observed:
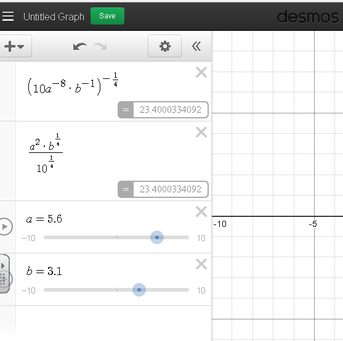
This week in my freshmen integrated math class, the students needed to review and comprehend laws of exponents. I created a sheet with three different types of problems (see figure below). I gave the students 5 minutes to read and annotate the document. Many of the comments I saw were pretty typical: "Why isn't the three inside the radical?", "Does eight to the zero just disappear?", "What does 16^(1/4) mean exactly?" The students then discussed with their groups the various questions and comments that they originally wrote down. As I listened to the conversations, I began to realize that the understanding of the concepts and rules of exponents was not going quite as I expected. One of the students asked me, "Mr. Watson, are you going to go over these?" Translation: "Mr. Watson, are you going to go up to the front and go through each one for us?" I did not think that going to the front and lecturing was the right thing to do at that point in time. Sure, I would go up and present the rules, answers, and be proud of the clarity of math that I shared with the students, but going by the old phrase 'the person doing the talking is the person doing the learning,' I realized at that point we needed a different direction as a class. In the past, I may have given in and spent the next twenty minutes spoon-feeding the information. Instead, I tried something different.  I asked the class the following question, "Which of you understand all nine problems, and no longer have questions?" Six students joined me at the front and I called them the 'group leaders.' At that point, I used the Team Shake app on my phone to generate six teams (it literally takes a few seconds to generate the teams). I then assigned one group leader per group. I explained to the group leaders that they needed to take their group to some space in the room to ask and answer questions about the different exponent rules and examples that we were learning about. All the groups went to various places around the room - some took small white boards for their group and some gathered around the large white board. The group leaders then began to ask and answer questions to their team. The conversations began to grow and soon the groups were off and running. I was sure to listen in as the groups discussed, debated, and collaborated on the problems and ideas. It was invigorating to say the least. I was a guide for the groups - giving proper direction when the groups veered off track, answering questions at the appropriate times, and ensuring that all team members were involved in the learning. When the groups told me they were 'finished', I gave them some extra practice problems. I had the group leaders come up so we could give them a round of applause for leading the groups. After that I told everybody to go back to their home tables, and I explained to them, "In your home tables, take a few minutes and formulate any lingering questions that you may have. You are going to have a chance to ask me these questions so be sure they are good ones!" The groups discussed for a few minutes and when I could tell they were ready, I set my timer for ten minutes. I then told them "You now have 10 minutes to ask me the lingering questions. Let's do this!" There were questions, but I found that they were much deeper than I had expected. Here are some examples:
I believe that both of these questions came to light because the mechanics and rules were discussed, explored, and answered in their groups. Then they had time to ask me more of 'wonder' type questions. 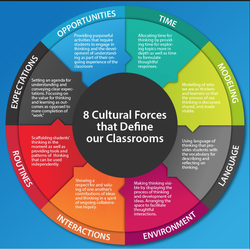 Which of the eight cultural forces were leveraged during this class period? Here is one view: Expectations: Student independence was actively cultivated by having them work in groups with group leaders and to be actively engaged with each other. The students directed most of the activity. Language: During the lesson, I tried to give specific action-oriented feedback, such as, "I like how you explained the fractional exponent rule here and the example that you used" and "This was a clever way to explain this to your group - it seemed like they really grasped the concept." Time: I really tried to monitor the amount of time that I talked during this lesson - it was limited to small chunks of time. The most that I was at the front talking at the class was the 10 minute session near the end. Interactions: Groups acted independently and many times I just listened in to hear their thinking. Many students challenged ideas, not the people pitching the ideas. Opportunities: Students got the opportunity to direct their own learning in their groups. The group leaders led the way, but all group members were allowed to questions and direct what was happening. In a previous article, I spoke of a "lawn" math classroom vs. a "ravine" math classroom. I believe that this class period was definitely exploring the "ravine!" At the 2017 Project Zero classroom in Cambridge, MA, David Perkins described a setting in which he was sitting on a well-manicured, perfectly green lawn, while a few feet away at the edge there existed a colorful, wild, interesting ravine, full of life and questions. He asked the participants: 'Is your classroom a lawn - well manicured, predictable, and neat, or is it a ravine - wild, messy, with organized chaos?'  This got me thinking about my own classroom, of course, and how for many years, my room primarily fit the description of a well-manicured 'lawn.' But what does a 'lawn' math classroom look like? What are its characteristics? I came up with a short list:
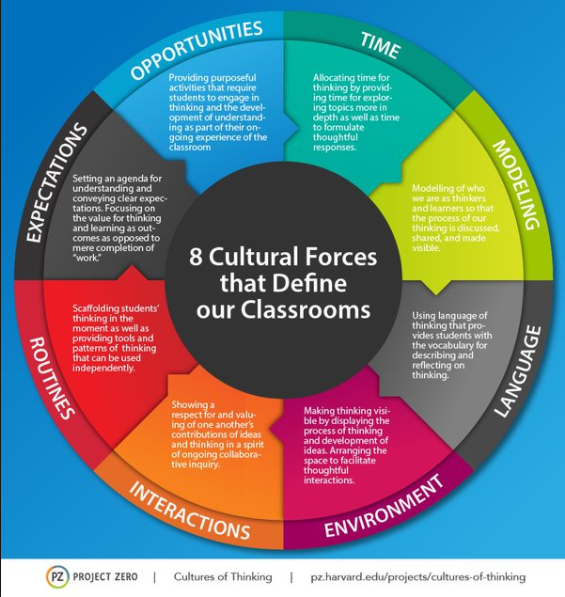
After thinking about this for a while, I remember an example math classroom from "Creating Cultures of Thinking: The 8 Forces We Must Master to Truly Transform Our Schools" by Dr. Ron Ritchhart, a member of the Project Zero team at Harvard University. In it, Dr. Ritchhart describes a math classroom in which he "had a hard time finding moments when students were truly engaged in any thinking" (Ritchhart, p. 39). The teacher was described as very personable, and was reliably consistent with her students, but that it seemed the students "made an internal calculation regarding how much attention needed to be paid to complete the homework successfully or prepare for the looming test" (Ritchhart, p. 40). This classroom seems to be primarily a 'lawn' classroom, with little, if any, ravine characteristics.  Now, to be clear, there is nothing inherently 'wrong' with a having a 'lawn' classroom some of the time, perhaps for part of a class period, or for an entire class period. There needs to be a good balance. The issue, in my opinion, is when a math classroom becomes a lawn day after day, and week after week, because this causes the teacher to do a majority of the critical thinking and the rich opportunities for student learning are lost. This idea of lawn versus ravine ties nicely with the eight cultural forces that make up the Cultures of Thinking (CoT) framework: expectations, language, time, modeling, opportunities, interactions, routines, and environment. If properly leveraged, the eight cultural forces could create a classroom culture that mimics the 'ravine', with some 'lawn'. However, if left to fester and not leveraged properly, the classroom could become primary a 'lawn', with little 'ravine': predictable, well-managed, but lacking the deep thought necessary for 21st century learning. So, how do the eight cultural forces 'look' in a math classroom that is primarily a 'lawn'? Let's take a look at each force: Expectations: Many things are expected of students in this type of classroom. The teacher may say things like:
Language: The key language moves to create a culture of thinking that Ritchhart describes are the language of thinking, community, identity, initiative, mindfulness, praise and feedback, and listening. In a 'lawn' classroom, some of these key language moves may not exist at all, or may be counter-productive to a culture of thinking. For example, if a teacher is continuously the sage and provider of information in a classroom, then students may never hear the language of community and identity. Furthermore, the language of praise and feedback may strictly be a language of praise without a language of feedback. Generic praise comments might include 'good job', 'great', 'brilliant', instead of action-oriented feedback such as 'I like how you completed the square here - I have not seen that before' or 'your graphs here are very detailed and it took very little time for me to get a clear picture of what is happening.' Time: In a lawn math classroom, time may be used very well and there may not be a second to spare, but the time spent may not be on critical thinking. For example, if a lot of time is spent in lecture or sit-and-get mode, then time is allocated and used, but students are merely scribes at that point, with little or no thinking being accomplished. If this is the case, there might not be enough time for students to process ideas. As a general rule, a teacher should not talk for more than ten minutes at a time in order to give students processing time. Modeling: The cultural force of modeling as described by Ritchhhart is the teacher as a role model of learning and thinking; in a lawn classroom the modeling may be predominantly instructional modeling which consists of the teacher showing techniques and methods to 'show the work' and 'get the right answer.' As a role model of learning, the teacher should be modeling how to take risks and reflect on the learning. It's ok for a math teacher to say, 'I'm not sure why dividing by 5 stretches the graph - I need to look into that more. It does seem like the graph should shrink. Why don't we do some research and we can talk about it next time and coordinate our ideas?' Opportunities: What opportunities are 'lawn' math classrooms providing for students? Ritchhart states that 'opportunities that teachers create are the prime vehicles for propelling learning in classrooms.' In 'lawn' math classrooms, the opportunities for rich thinking in which the student examines, notices, observes, identifies, uncovers complexities, and captures the essence of something may be limited. If a math classroom consists of homework check followed by direct instruction, day in and day out, then it is very possible that a student does not think at all, outside of the elementary tasks of 'paying attention' and 'taking notes.' As a math teacher, do you take quality time when planning to ensure that your students have rich opportunities?  Interactions: A 'lawn' math classroom may consist of a lot of QRE interactions, which stands for Question-Respond-Evaluate - the teacher asks a question, a student responds, then the teacher evaluates that answer. This results in a 'Ping-Pong match back and forth between the teacher and a single student, leaving much of the class out of the interaction' (Ritchhart, p. 212-13). The interactions that should be fostered are ones where the students are pushed to reason and think beyond a simple answer. Routines: A 'lawn' math classroom may be littered with procedural routines, for example:
 Environment: Take a look at the image created by Thomas Murray ([email protected]) on the left. Does this look familiar? Not much has changed if you compare the class from 1916 to the one from 2016, yet the world around us has changed in so many ways. In many math classrooms, desks in rows are still a reality. Is there a place for this? Sure there is, perhaps during tests or at a time where a mathematical procedure needs to be shown. However, this should not be the primary setup; it should be changed to allow students to have richer learning opportunities, interactions, collaborations, and discussions. So, what is a 'ravine', and what do the eight forces 'look' like in that type of classroom? Stay tuned as I will look at that in the next blog post!  David Perkins spoke on the last day of the institute about how to take these ideas back to our schools. He mentioned the 5-year effect: new ideas get implemented, get traction, then slowly lose that energy and eventually die off. So, how do we make sure the energy does not fall away, and that key ideas and frameworks can have a long life? One thing that many schools do use is what Perkins calls the "installation model" of implementing change. Some training happens, maybe posters and brochures are made, teachers implement it, but then over time things begin to change back to the way they were. How do we combat this and ensure longevity? David talks about the "ecological model" of introducing change which has 4 main "legs":
Please check out the full article on "Giving Change Legs"
Wow! What a week! Things are beginning to wind down here in Cambridge and will culminate tomorrow when Tina Blythe and David Perkins, both of the Project Zero team, give a talk on "Giving Change Legs," which I believe will help us to utilize many of the awesome things we have learned here this week. First I included a few pictures. Then I include some discussion on the course "All Learners Learning Every Day."
All Learners Learning Every Day (ALL-ED) by Rhonda Bondie
Key takeaways:
Creating a Culture of Thinking right from the start
Creating thinking opportunities from a mathematics perspective What is a color, symbol, and image that captures the Project Zero classroom thus far? Here is my take! Color: Yellow - I chose yellow because I think yellow represents energy, brightness, and excitement. These qualities have been on display here for two days!  Symbol: No spoon feeding - I believe that to use many of the great ideas presented here at project zero effectively, spoon feeding of students needs to be kept to a minimum. In math class, spoon feeding can take many forms, such as: showing them the recipe to do a math problem as opposed to the students creating the recipe; giving them the answers to a set of questions as opposed to them using other tools to gather the answers, such as Wolfram Alpha, Desmos, or each other; handing them a review sheet of problems that will be on the test as opposed to them coming up with the ideas and concepts that they will be tested on, to name a few.  Image: An awesome buffet - A great buffet, like the one shown at the right, presents a lot of appealing options. We have the freedom of choice to pick the items that we like the most, and also to leave what we won't eat. We also can go back to the buffet later, and pick items that we want again, or new items. This institute reminds me of that because we have been presented with a plethora of appealing ideas, many of which we want to take, and some that we may not be ready for. We have the freedom of choice to pick the ideas that we want to try to implement, and ones that we may want to come back to later. Slow LookingDefinition of Slow-looking: Taking time to notice more than meets the eye at first glance The themes of slow looking
 I was thinking about the applications to math class, and at first was a bit puzzled as to what that would look like. After discussing it with my study group (STUDY GROUP O ROCKS!), the slow-looking does not have to involve an image, it could be a writing, a poem, an image, or work from a math problem. Many times in class, students will use a solution guide for a math problem, and after a minute or to proclaim, 'I have no idea what they are doing here!' It is in this instance that I think I will walk them through 'slow-looking' at the solution, and remind them of the quote to the left! The Teaching for Understanding (TfU) framework We assume we teach for understanding because we equate knowledge and understanding; knowledge is vital and critical, but just having a lot of knowledge doesn't make for understanding. What is it that a child will be able to do better if they understand? The goals of the Teaching for Understanding framework:  What does it mean to understand? Identify something that you understand really well. For me, it was finding solutions of a quadratic equation. My evidence is that I can find the solutions in multiple ways; I know what the solutions look like; all methods of solving result in the same solutions. What does understanding look like? 1. successful at something 2. know the pattern of doing things 3. you can teach it well 4. can analyze into component part and synthesize into whole 6. big picture in relation to details 7. anticipate 8. you can make connections 9. have a greater metacognition 10. can problem solve 11. can do it in a variety of ways What helps understanding develop? - doing multiple times - errors, mistakes, mishaps - mentor, guide, structure - explain it to someone - deconstructing - curiosity - exploring various ways to do something - observe - different perspectives - reflection - applying, implementing - try it again and again  What does teaching for understanding look like in the classroom? Some of the key questions from our study group today:
|
Archives
February 2021
Categories
All
AuthorJeff Watson is a Math teacher at the University Liggett School in Grosse Pointe Woods, MI. His work as a software engineer made him realize the need for problem solvers and critical thinkers in the workplace today. Jeff believes that the secondary math classroom should be a place of critical thinking, collaborative learning, and exploration which will cultivate the problem solvers and thinkers needed today. |




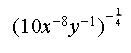





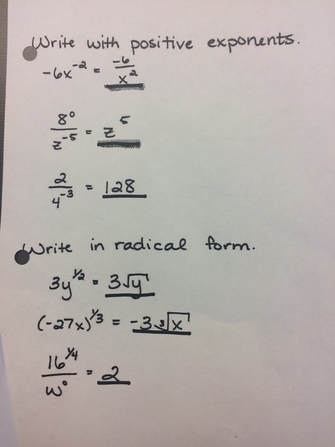

































































 RSS Feed
RSS Feed
